Menon

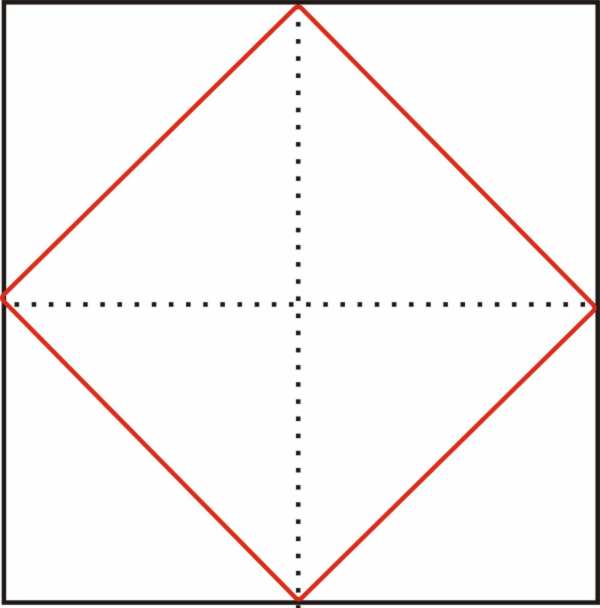
Menon ist ein Platondialog, in dem es zunächst um ethische Fragen Menons, zunehmend aber um das von Sokrates selbst bis zur Aporie (Ausweglosigkeit) des Menon getriebene Erkenntnisproblem des Definierens selbst geht, und zwar in folgender Stufung der Untersuchungsebenen: "Ist Tugend lehrbar?", "Was ist Tugend?", "Wie läßt sich überhaupt etwas definieren?", "Kann ich etwas suchen, dessen Definition ich noch nicht kenne?" Letztere Frage wird von Sokrates mit Ja beantwortet, denn sonst gäbe es gar kein Fragen und Forschen und auch keine Erkenntnis. Allerdings seien die Antworten im Suchenden selbst verborgen und müssten durch die Ausweglosigkeit, die Aporie des Suchers, gewissermaßen herausgefordert werden. Solange der Mensch die Antwort ungeprüft und unverteidigt zu kennen glaubt, reizt ihn nichts zur Suche; die Erkenntnis des eigenen Ungenügens, der Schmerz der Aporie, veranlasst ihn zu wissenschaftlicher Unermüdlichkeit, zu eigentlicher, weit aufgespannter Frageoffenheit.

Sokrates zeigt die Folge von scheinbarem Wissen, Aporie und Anamnesis, d.h. erinnerungsartiges Hervorholen des im Seeleninnern verborgenen Wissens, durch ein pädagogisches Experiment mit einem Pflegejungen bzw. Sklaven (griech. "pais") des Menon auf, den er danach befragt, wie sich ein Quadrat so verdoppeln lässt, dass wiederum ein Quadrat (also das doppelt so große) herauskommt. Das Ausgangsquadrat soll zwei mal zwei Fuß groß sein, das resultierende Quadrat muss demnach acht Quadratfuß groß sein. Wie groß ist aber dessen Seitenlänge?

Da der Flächeninhalt acht Fuß beträgt, denkt der Junge, die Seite müsse vier Fuß lang sein. Dies ergäbe allerdings eine Vervierfachung der Fläche; der Junge wählt nun einen scheinbaren Mittelwert von drei Fuß, aber das Quadrat über drei Fuß hat eine Fläche von neun, nicht von acht Quadratfuß. So erreicht der Sklave die aporetische Einsicht, es bisher noch nicht gewusst zu haben.

Sokrates führt den Jungen nun in kleinschrittigen Rückfragen zu einer schlichten zeichnerischen Lösung, die es dem, der sie sieht, wie Schuppen von den Augen fallen lässt: Halbierung des Ergebnisquadrats von acht Quadratfuß ist ja durch die Diagonale möglich; diese Diagonale zieht er aber nicht durch die Mitte des ganzen, sondern durch die vier Viertel des Achtfußquadrats; das dadurch umschriebene Mittelquadrat ist Quadrat auf der Diagonalen je eines der Viertel. Das große ist wiederum Quadrat auf der Diagonalen des aus den Vierteldiagonalen gebildeten Binnenquadrats.

Kurz: Verdopplung eines Quadratinhalts wird dadurch erreicht, dass man das Quadrat auf der Diagonale des Ausgangsquadrates bildet.

Da der Junge nie in Geometrie unterrichtet wurde, muss er dieses Wissen schon vor dem Erinnerungsfeld dieses jetzigen Lebens erlernt haben, sei es in der vorgeburtlichen himmlischen Weisheit, sei es in früheren Leben und ihren unendlichen Erfahrungen, so dass er dieses erworbene Wissen wie eine Erinnerung wieder hervorholen konnte. Allgemeingültige Sätze wie die der Geometrie sind als Bewusstseinsstrukturen im Menschen bereits angelegt, sie sind, so würde es Kant zweitausendzweihundert Jahre später formulieren und gleichfalls an Geometriebeispielen verifizieren, a priori.

Weblink

Platons Dialog Menôn griechisch / deutsch