|
|
Im ptolemäischen Weltsystem der Astronomie wurde die Epizykeltheorie eingeführt, um Änderungen von Geschwindigkeit und Richtung der scheinbaren Bewegungen von Mond, Sonne und Planeten am Himmel zu erklären. Sie wurde vermutlich von Apollonios von Perge gegen Ende des 3. Jahrhunderts v. Chr. aufgestellt. Insbesondere versucht sie, die retrograde (rückläufige) Bewegung von Planeten zu erklären. Das Weltbild der damaligen Zeit war durch die Lehre des Aristoteles bestimmt, nach der die Erde im Zentrum des Universums steht, die Planeten auf Kristallsphären befestigt sind und sich gleichförmig um den Mittelpunkt bewegen (geozentrisches Weltbild). Nach Aristoteles sind alle Bewegungen außerhalb der Mondbahnsphäre unveränderlich und vollkommen, und verlaufen damit auf perfekten Kreisbahnen. Theorie
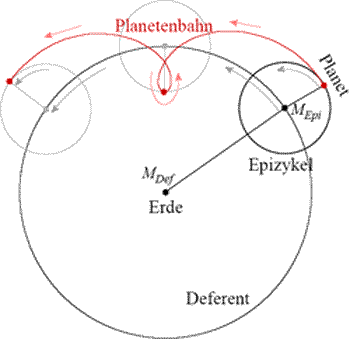
Schleifenbahn eines Planeten nach der Epizykeltheorie Ptolemäus versuchte, die aristotelische Lehre mit den widersprüchlichen Beobachtungen in Einklang zu bringen und schuf deshalb ein Rechenmodell auf Basis der Epizykeltheorie. Nach der Epizykeltheorie bewegen sich die Planeten entlang eines kleinen Kreises, des Epizykels (griech. epíkyklos, »Nebenkreis«), der sich seinerseits wiederum entlang eines größeren Kreises, des Deferents (auch deferierender Kreis; von lat. deferre, »übertragen«), bewegt. Die Bewegung entlang der Kreise erfolgt jeweils in östlicher Richtung und etwa parallel zur Ebene der Erdumlaufbahn (Ebene der Ekliptik). Die Bahnen der Planeten in diesem System sind Epizykloiden. Im Mittelpunkt des Deferents befindet sich der Theorie nach die Erde. Von ihr aus gesehen würden sich nun die Planeten meist nach Osten in Richtung des Deferents bewegen. Die Hälfte der Zeit summiert sich zu dieser Bewegung auch die ostwärts gerichtete Bewegung auf dem Epizykel. Die andere Zeit aber liefe der Planet auf dem Epizykel entgegengesetzt zur Bewegung des Deferenten, wodurch sich seine Bewegung am Himmel verlangsamen und schließlich in eine retrograde übergehen würde, durch die die Planetenbahn schließlich eine Schleife vollführte. Dieser „Rechentrick“ reichte aber nicht aus, die Bewegung der Planeten vollständig zu erklären. So war es notwendig, weitere Stufen von Epizykeln hinzuzufügen (Epizykel auf Epizykeln). Die Epizykeltheorie wurde außerdem spätestens von Ptolemäus mit der Exzentertheorie Hipparchs verbunden, d. h., die Erde wurde aus dem Zentrum des Deferents verschoben. Ferner führte Ptolemäus den Äquant ein, den scheinbaren Mittelpunkt der gleichförmigen Kreisbewegung, der weder mit dem Mittelpunkt der Kreisbahn noch dem Standpunkt der Erde übereinstimmt. Die Berechnung der Bahnen wurde damit allerdings äußerst kompliziert. Überwindung der Epizykeltheorie Das heliozentrischen Weltbild erklärt die Schleifen der Planetenbahnen durch Überlagerung mit der Erdbewegung und scheint deshalb auf Epizykel verzichten zu können. Da das neue Modell aber immer noch von kreisförmigen Umlaufbahnen für die Planeten ausging, mußten Unstimmigkeiten wieder durch Verwendung der Epizykel erklärt werden. Kopernikus verwendete in seinem Weltsystem immer noch 34 Epizykel, konnte aber eine schlüssige Erklärung liefern für die Bindung der Merkur- und Venusbahn an die Sonne. Erst durch Johannes Kepler wurde die Epizykeltheorie überflüssig: Das „natürliche“ Modell der Planeten auf ellipsenförmigen „Keplerbahnen“ um die Sonne benötigt keine Korrektur durch überlagerte Epizykel. Siehe auch: Keplersche Gesetze Von "http://de.wikipedia.org/"
 |
||||||||||||||||||